Liars Dice is a game for two or more players.  During a hand, each player rolls a set of die (typically starting the game with 5 die per player) under a cup to shield their hand from the other players.  Each player then progressively makes ever increasing bids as to the number of die of a certain face value that are contained in everyone’s collective hands.  The bid is based on what each player can see in their hand and the number of concealed die in the other players hand.  The hand starts with one player bidding on the number of die displaying a particular face value ( i.e. there is one die displaying a face value of 3,  or there is 1 – 3).   The next player must either raise the bids quantity or face value higher (i.e. there is 1 – 4, 2 – 3’s, etc) or challenge the prior bid by calling the other player a liar.  Once a player is called a liar, everyone’s hand is revealed and the bid is evaluated.  If the bid is higher than the number of die of the particular face value, then the bidder loses and must remove a die from his or her hand. However, if the number of die of a particular face value exceeds that of the bid, then the challenger loses and must remove a die from his or her hand.  This process repeats until there is only one person with die in their hand and this person is declared the winner.

The challenging portion of this game is determining what to raise the bid to and when to challenge another player’s bid.  For each die there is a 1 in 6 chance that a particular face value will be rolled;  however, the number of die with a particular face value is difficult to estimate even with the knowledge of the face values of the die in your own hand.  Plus as the game progresses, the number of die in circulation is progressively decreased changing the odds.  It is much more likely that there are at least 2 – 6’s when there is 20 die in circulation than when there are only 2 die in circulation.  It is also much more likely that there are at least 2 – 6’s than 20 – 6’s when there is 20 die in circulation.

Applying Excel’s BINOMDIST() Function

Excel’s BINOMDIST(x, n, p, cumulative) function returns the probability of “x” or fewer successes in “n” independent trials given a probability of success of “p”, when “cumulative” is true.  This function can be modified as follows such that it returns the probability of “x” or more successes in “n” independent trials given a probability of success of “p” when cumulative is true.  Using this equation, one may calculate the probability of “x” or more die being rolled with the same face value out of “n” total die rolled given the probability of a single die rolling a particular face value “p”.

P(x or more successes) = 1 - BINOMDIST(x - 1, n, p, cumulative)

Where:

x = bid for number of die with a particular face value (in addition to what's in you hand)
n = number of die in circulation (not in your hand)
p = probability of a single die rolling a particular face value
cumulative = True (Returns the CDF)

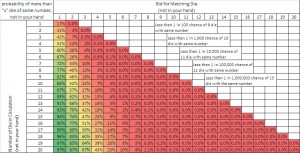
Liars Dice Bidding Probability (No Wilds)

The previous equation was used to calculate the probability that a particular bid is correct based on the number of die in circulation. The probability of a single die rolling a particular face value is 1 in 6, or 16.66%.  The resulting probabilities for varying bids and quantities of die in other players hands have been listed in the table below and color coded such that 0% chance is red, 50% chance is yellow, and 100% chance is green.

Example Bid (How to interpret the table): 

If you are playing with 3 other people (5 die per player) then there are 15 die in your opponents hands.  Based on the chart above, there is a 47% chance that 3 or more of the 15 die in your opponents hands will have a particular face value.  If you happen to be dealt 2 – 2’s, then you might bid 5 – 2’s and you would have a 47% chance of being correct.

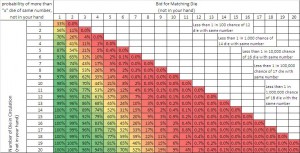
Liars Dice Bidding Probability (Single Wild)

One popular variation of the game is to make a particular face value wild (traditionally the 1’s). The probability of a single die rolling a particular face value is 1 in 3, or 33.33% (due to the wilds). The resulting probabilities for varying bids and quantities of die in other players hands have been listed in the table below and have been color coded such that 0% chance is red, 50% chance is yellow, and 100% chance is green.

Example Bid (How to interpret the table): 

If you are playing with 3 other people (5 die per player) then there are 15 die in your opponents hands.  Based on the chart above, there is a 60% chance that 5 or more of the 15 die in your opponents hands will have a particular face value.  If you happen to be dealt 2 – 2’s, then you might bid 7 – 2’s and you would have a 60% chance of being correct.

Before you leave don’t forget to:

• Subscribe to the blog in the right side panel.
• Share this article with your friends!
• Leave a comment
• Tell Kevin that I will beat him at this game! … eventually. 🙂